Embark on a journey to unravel the mysteries of linear equations, delving into the realm of ‘which equation describes this line.’ In this exploration, we’ll uncover the diverse types of equations that govern lines, their defining characteristics, and the significance of their parameters.

Unveiling the secrets of equation representation, we’ll learn to translate between different forms, appreciating the nuances of each. Moreover, we’ll decipher the language of equations, interpreting their parameters to reveal the geometric and algebraic properties of the lines they describe.

Equation Types

Various types of equations can describe a line. Each type possesses unique characteristics, advantages, and disadvantages. Understanding these differences aids in selecting the most appropriate equation for a given situation.

Slope-Intercept Form

• Equation: y = mx + b
• Key characteristics: Defines a line using its slope (m) and y-intercept (b).
• Advantages: Easy to interpret, widely used, and allows for quick calculation of slope and y-intercept.
• Disadvantages: Not suitable for vertical lines (slope is undefined).

Point-Slope Form

• Equation: y – y ₁= m(x – x ₁)
• Key characteristics: Defines a line using a given point (x ₁, y ₁) and its slope (m).
• Advantages: Useful when a point on the line and its slope are known.
• Disadvantages: More complex to manipulate compared to slope-intercept form.

Standard Form

• Equation: Ax + By = C
• Key characteristics: Defines a line using coefficients A, B, and C, where A and B represent the slopes in the x and y directions, respectively.
• Advantages: Useful for finding the x- and y-intercepts.
• Disadvantages: Less intuitive than slope-intercept form.

Equation Parameters

Equations used to describe lines typically involve several parameters that determine the line’s shape and position. These parameters provide specific information about the line’s orientation, slope, and location in the coordinate plane.

The most common parameters used in line equations are:

Slope (m)

The slope of a line measures its steepness or incline. It is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate as you move along the line. A positive slope indicates an upward-sloping line, while a negative slope indicates a downward-sloping line.

Y-Intercept (b)

The y-intercept of a line is the point where the line crosses the y-axis. It represents the value of y when x is equal to zero. The y-intercept determines the vertical position of the line in the coordinate plane.

X-Intercept (a)

The x-intercept of a line is the point where the line crosses the x-axis. It represents the value of x when y is equal to zero. The x-intercept determines the horizontal position of the line in the coordinate plane.

Equation Form, Which equation describes this line

The equation of a line can be expressed in different forms, including the slope-intercept form (y = mx + b), the point-slope form (y – y ₁= m(x – x ₁)), and the standard form (Ax + By = C).

The choice of equation form depends on the information available about the line.

3. Equation Representation

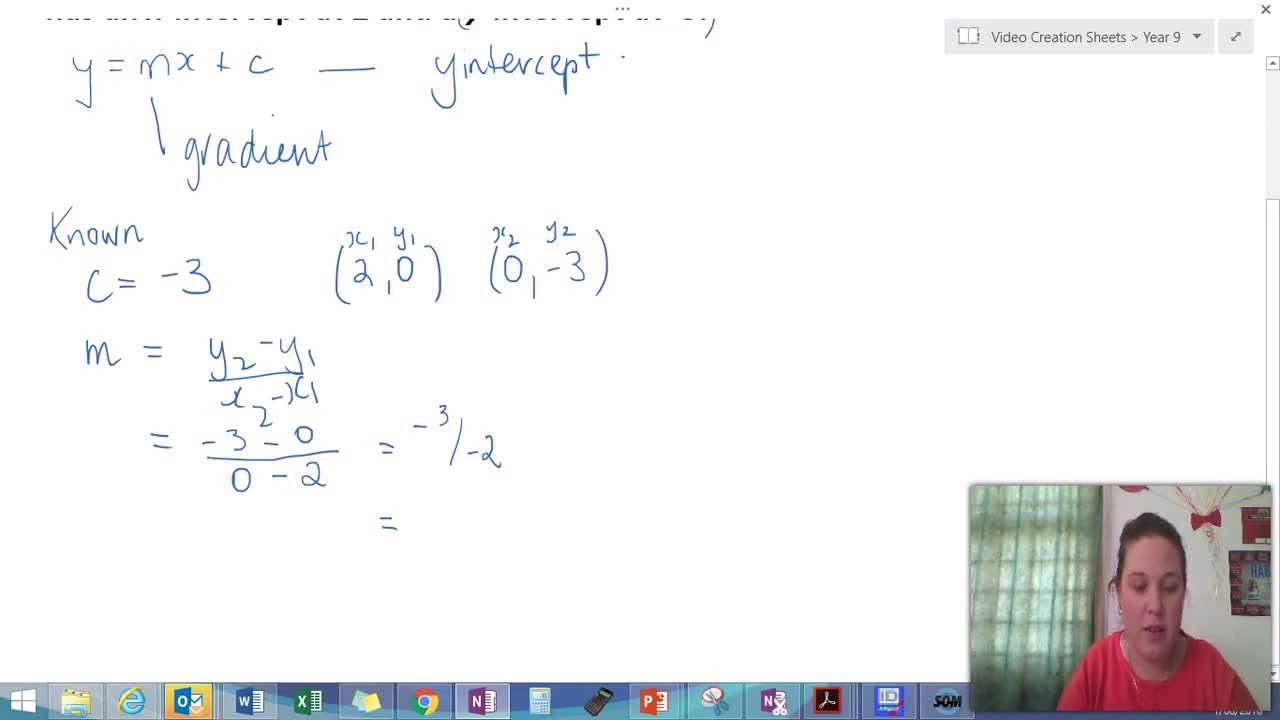
Different equation representations provide alternative ways to describe a line, each with its own advantages and applications. Understanding the different representations and the steps involved in converting between them is essential for effectively working with lines in various mathematical and real-world contexts.

Equation Forms

There are several common equation forms used to represent lines:

• Slope-intercept form: y = mx + b
• Point-slope form: y – y1 = m(x – x1)
• Standard form: Ax + By = C

The slope-intercept form is often the most convenient for finding the slope and y-intercept of a line. The point-slope form is useful when you know a point on the line and its slope. The standard form is commonly used in applications where the coefficients A, B, and C have specific meanings or constraints.

Converting Between Forms

Converting between different equation forms involves solving for the appropriate variables. For example, to convert from slope-intercept form to standard form, you can rearrange the equation as follows:

y = mx + by

mx = b

Ax + By = C (where A =

m and B = 1)

Similarly, you can convert from point-slope form to standard form by substituting the point (x1, y1) and slope m into the standard form equation and solving for C.

Choosing the Appropriate Representation

The choice of equation representation depends on the specific application. For instance, the slope-intercept form is convenient for graphing a line, as it directly gives the slope and y-intercept. The point-slope form is useful for finding the equation of a line passing through a given point with a known slope.

The standard form is often used in systems of equations and other algebraic manipulations.

4. Equation Interpretation

The parameters of an equation provide valuable insights into the properties of the line it describes. These parameters determine the slope, y-intercept, and orientation of the line, which have significant geometric and algebraic implications.

Geometric Implications

• Slope (m): The slope represents the steepness of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. The greater the absolute value of the slope, the steeper the line.
• Y-intercept (b): The y-intercept represents the point where the line crosses the y-axis. It determines the vertical displacement of the line from the origin.

Algebraic Implications

• Point-slope form: This form is particularly useful when a point on the line and its slope are known. The equation is expressed as y- y ₁= m(x – x ₁) , where (x ₁, y ₁) is the given point and m is the slope.

• Slope-intercept form: This form is commonly used when the slope and y-intercept are known. The equation is expressed as y = mx + b, where m is the slope and b is the y-intercept.

Solving Problems

Equations of lines can be used to solve a variety of problems, such as:

• Finding the equation of a line given two points
• Determining whether two lines are parallel or perpendicular
• Finding the point of intersection between two lines

5. Equation Applications: Which Equation Describes This Line

Equations play a vital role in describing lines, providing a concise and precise mathematical representation of their properties. These equations find applications in various fields, including geometry, physics, and engineering, enabling us to solve complex problems and gain insights into the behavior of lines.

Geometry

• Determining the slope and y-intercept of a line
• Calculating the angle between two lines
• Finding the equation of a line passing through two given points
• Classifying lines as parallel, perpendicular, or intersecting

Physics

• Describing the trajectory of a projectile
• Calculating the velocity and acceleration of an object in motion
• Determining the relationship between force, mass, and acceleration

li>Modeling the behavior of waves and other physical phenomena

Engineering

• Designing bridges and other structures
• Creating computer-aided design (CAD) models
• Analyzing the stability of systems
• Simulating the behavior of electrical circuits

For example, in civil engineering, equations are used to calculate the load-bearing capacity of bridges, ensuring their safety and stability. In electrical engineering, equations describe the flow of current and voltage in circuits, helping engineers design efficient and reliable systems.

Quick FAQs

What is the most common type of equation used to describe a line?

The slope-intercept form (y = mx + c) is widely used for its simplicity and intuitive interpretation.

How do I determine the slope of a line from its equation?

In the slope-intercept form (y = mx + c), the coefficient of x (m) represents the slope.

What is the significance of the y-intercept in a line equation?

The y-intercept (c) indicates the point where the line intersects the y-axis.