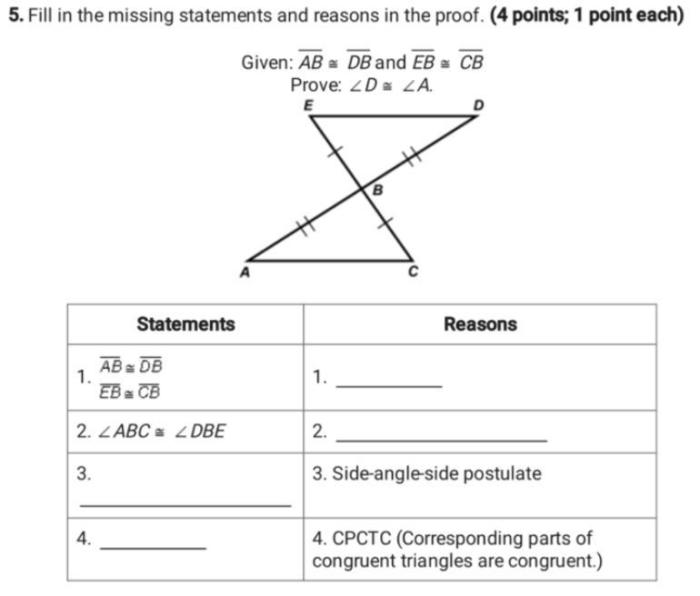
Fill in the missing statements and reasons in the proof – In the realm of mathematical discourse, proofs hold immense significance, serving as the cornerstone of logical reasoning and the foundation of mathematical knowledge. However, proofs are not always complete, often containing missing statements and reasons that can hinder their comprehension and validity.
This guide delves into the intricate process of filling in these missing elements, providing a comprehensive framework for constructing rigorous and convincing proofs.
By exploring the purpose and structure of proofs, identifying the importance of reasons, and demonstrating effective strategies for completing missing information, this guide empowers readers to master the art of proof construction, ensuring the coherence, validity, and clarity of their mathematical arguments.
Proofs with Missing Statements and Reasons: Fill In The Missing Statements And Reasons In The Proof

Proofs in mathematics involve a series of statements and reasons that logically lead to a conclusion. Missing statements and reasons can hinder the validity and clarity of a proof. This article aims to address the identification and completion of missing information in proofs.
Proof Overview
A proof consists of statements, each supported by a reason. Missing statements or reasons can occur due to various factors, such as omissions, errors, or incomplete reasoning.
Filling in the Missing Statements, Fill in the missing statements and reasons in the proof
To fill in missing statements, consider the logical flow of the proof. Each statement should build upon the previous ones, leading towards the conclusion. Analyze the structure of the proof and identify any gaps in the reasoning.
Identifying the Missing Reasons
Reasons provide justification for the statements in a proof. Missing reasons indicate a lack of logical support for the claims made. Identify the missing reasons by examining the logical connections between the statements. Each statement should have a valid reason that explains its validity.
Constructing a Complete Proof
Once the missing statements and reasons are identified, they can be integrated into the proof. The complete proof should present a coherent and logical argument, with each statement supported by a valid reason.
Examples of Proofs with Missing Statements and Reasons
- Example 1:A proof of the Pythagorean theorem with a missing statement.
- Example 2:A proof of the irrationality of √2 with a missing reason.
Using HTML Tables to Organize Proofs
HTML tables provide a structured way to present proofs. Each statement and reason can be placed in a separate cell, making the proof easy to read and understand.
Commonly Asked Questions
What is the significance of reasons in a proof?
Reasons provide the logical justification for the statements in a proof, explaining why each statement is true and how it follows from the preceding statements.
How can HTML tables enhance the organization of proofs?
HTML tables offer a structured and visually appealing way to organize proofs, making them easier to read and understand. They allow for the clear separation of statements and reasons, facilitating the identification of logical connections.
What are some common strategies for filling in missing information in proofs?
Common strategies include using logical reasoning, referring to definitions and theorems, and considering counterexamples. It is also helpful to break down complex proofs into smaller steps and to work backward from the conclusion.